Formulas for evaluating racquet performance
The math involved in the derivations is high school algebra. The conservation principles applied are first year physics.
- Conservation of angular momentum
- Conservation of linear momentum
- Axis of rotation
- Benchmark conditions for objective racquet comparisons
- Coefficient of restitution
- Elbow Crunch (Elbow Yank)
- Impact Force (impulse force)
- Impulse Reaction
- Kinetic energy
- Moment
- New Balance Point
- The Parallel Axis Theorem (P.A.T.)
- Shock
- Shoulder Crunch
- Shoulder Pull
- Sweet Spot
- Tip Speed
- Torque
- Torsion (Longitudinal torque)
- Units of measurement and conversion factors
- Variables
- Work (kinetic energy)
- Wrist Crunch
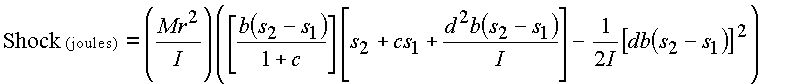
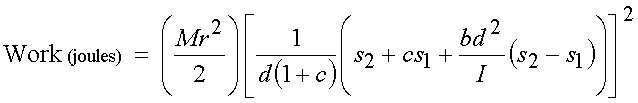
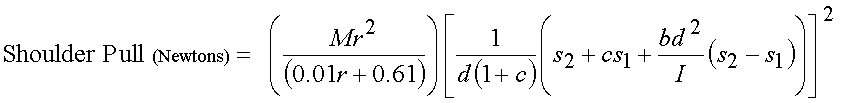
\[ Shoulder\ Crunch\ (Newtons) = \frac{2}{0.01r + 0.61} \times Shock \]
Derivation
\[ Elbow\ Crunch\ (Newtons) = \left(\frac{2}{0.01r + 0.36}\right) \times Shock \]
Derivation
\[ Wrist\ Crunch\ (Newtons) = \left(\frac{2}{0.01r + 0.08}\right) \times Shock \]
\[ Tip\ Speed\ (m/s) = \sqrt{\frac{2}{M} \times Work \times \frac{e}{r}^2} \]
\(e\) = distance from axis to tip, in cm Derivation
The \(Impact\ Force\) in Newtons acting at mass center due to impact.
\[ Impact\ Force = \frac{M}{t} \times \left[(1 + c) \times \sqrt{\frac{2}{M} \times Work} - \frac{r}{d} \times (cs_1 + s_2)\right] \]
Derivation
| \(A_x\) | = | Impulse Reaction, the translational force acting at the axis of rotation due to impact, in Newtons. Note that when \(d\) = \(q\) (\(q\) is the distance from the axis of rotation to the center of percussion), the expression within the second set of parentheses becomes zero. |
| \(a\) | = | linear acceleration of the mass center, in m/s² |
| \(b\) | = | mass of the ball, in kg |
| \(c\) | = | coefficient of restitution of the racquet/ball system |
| \(d\) | = | distance from the axis of rotation to the impact point, in cm |
| \(e\) | = | the distance from the axis of rotation to the tip |
| \(F\) | = | force applied at mass center, in Newtons |
| \(I\) | = | moment of inertia (swing weight) of racquet, in kgf/cm² |
| \(I_5\) | = | moment of inertia (swing weight) of racquet at 5cm from the butt, in kgf/cm² |
| \(I_7\) | = | moment of inertia (swing weight) of racquet at 7cm from the butt, in kgf/cm² |
| \(I_{10}\) | = | moment of inertia (swing weight) of racquet at 10cm from the butt, in kgf/cm² |
| \(I_a\) | = | moment of inertia (swing weight) of racquet at distance \(a\) from the butt, in kgf/cm² |
| \(M\) | = | mass of the racquet, in kg |
| \(m\) | = | mass in kg |
| \(ω\) | = | angular velocity of racquet, in radians/s |
| \(p\) | = | linear velocity of impact point, in m/s |
| \(r\) | = | distance in cm from mass center (balance point) to axis used in the stroke |
| \(s\) | = | ball velocity, in m/s (positive is away from player) |
| \(s_1\) | = | velocity of ball before impact, in m/s |
| \(s_2\) | = | velocity of ball after impact, in m/s |
| \(T\) | = | torque at axis of rotation, in Nms |
| \(t\) | = | dwell time, or duration of impact, in seconds |
| \(v\) | = | linear velocity of the mass center, in m/s |
| \(v_1\) | = | linear velocity, just before impact, of racquet mass center, in meters/second |
| \(v_2\) | = | linear velocity, just after impact, of racquet mass center, in meters/second |
See also: Units of measurement and conversion factors.