Formula: Torque
The impact of a ball with a racquet is a case of eccentric impact,
so both rotation (turning about the axis of rotation, at the middle of the hand) and translation (movement of the axis of rotation backwards or forwards) result from the collision. In other words, the hand will be both pulled and twisted when the ball hits the racquet. These resultant forces from impact should be minimized.
Torque and Impulse Reaction are the two resultant forces from an eccentric impact, such as the collision of a tennis ball with a racquet face.
\[ Torque\ (Newton.meters) = \left(\frac{Mr^2}{I}\right) \left(\frac{db(s_2 - s_1)}{100t} \right) \]
Torque is the twist back on impact, measured in units of Nm. Derivation of a formula for Torque requires application of the principle known as Conservation of Angular Momentum. Unlike energy, momentum is conserved in any collision. Momentum is of two types: linear (straight line) and angular (rotating about an axis of rotation). If we pick any point (such as the axis of rotation 7 cm from the handle end), and sum up all of the angular momenta before impact, this sum will remain the same after impact even though the angular momenta of the ball and racquet have changed. See the explanation of why the torque of the player during impact can be disregarded when writing the conservation equation. A complete description of all variables used in this derivation follows at the end.
During the impact, there is also a force involved which is external to the racquet/ball system. This external force is a torque, or turning force, contributed by the player at the axis of rotation. But this is a non-impulsive force, therefore it is disregarded. Because the angular momentum contributed by this external force is small due to the short time that any angular acceleration of the racquet has to work, we can omit this external angular impulse from the conservation of angular momentum equation. Note on this assumption.
The angular momentum of the racquet is its swingweight (\(I\)) × its angular velocity (\(w\)); the angular momentum of the ball is its mass (\(b\)) × its velocity (\(s\)), × the distance (\(d\)) from the axis of rotation to the point of impact. From the equation arising from this conservation principle, derive an expression for the resultant angular impulse due to the racquet and ball alone, regardless of external forces. Note on this assumption.
The expression for the angular impulse due to the impact of the ball with the racquet is \(I(w_1 - w_2)\). From this, get the change in angular velocity of the racquet during the impact \((w_1 - w_2)\) (in radians per second). See the derivation. Multiplying the change in angular velocity by the distance (r) from the axis of rotation to the mass center, or balance point, will give the difference in linear velocities, before and after impact, of the racquet’s mass center. Then dividing the difference in linear velocities by the time of impact will give the deceleration of the racquet’s mass center. By Newton’s Second Law, the deceleration of a mass is a force, so the result of multiplying a mass by a deceleration is a negative force in Newtons. Multiplying this force by its lever arm (\(r\)) gives the Torque resulting from impact. This Torque is a twist on the hand, backward, with the axis of rotation between the middle and ring fingers.
Applying Conservation of Angular Momentum, with \(d\) and \(I\) in centimeters:
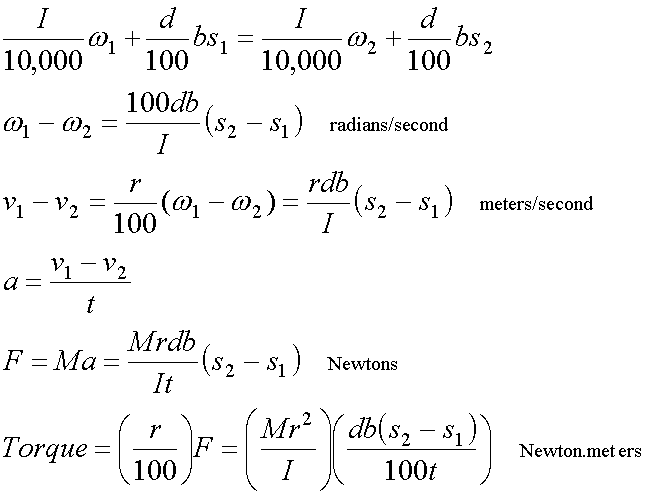
| \(A_x\) | = | Impulse Reaction, the translational force acting at the axis of rotation due to impact, in Newtons. Note that when \(d\) = \(q\) (\(q\) is the distance from the axis of rotation to the center of percussion), the expression within the second set of parentheses becomes zero. |
| \(a\) | = | linear acceleration of the mass center, in m/s² |
| \(b\) | = | mass of the ball, in kg |
| \(c\) | = | coefficient of restitution of the racquet/ball system |
| \(d\) | = | distance from the axis of rotation to the impact point, in cm |
| \(e\) | = | the distance from the axis of rotation to the tip |
| \(F\) | = | force applied at mass center, in Newtons |
| \(I\) | = | moment of inertia (swing weight) of racquet, in kgf/cm² |
| \(I_5\) | = | moment of inertia (swing weight) of racquet at 5cm from the butt, in kgf/cm² |
| \(I_7\) | = | moment of inertia (swing weight) of racquet at 7cm from the butt, in kgf/cm² |
| \(I_{10}\) | = | moment of inertia (swing weight) of racquet at 10cm from the butt, in kgf/cm² |
| \(I_a\) | = | moment of inertia (swing weight) of racquet at distance \(a\) from the butt, in kgf/cm² |
| \(M\) | = | mass of the racquet, in kg |
| \(m\) | = | mass in kg |
| \(ω\) | = | angular velocity of racquet, in radians/s |
| \(p\) | = | linear velocity of impact point, in m/s |
| \(r\) | = | distance in cm from mass center (balance point) to axis used in the stroke |
| \(s\) | = | ball velocity, in m/s (positive is away from player) |
| \(s_1\) | = | velocity of ball before impact, in m/s |
| \(s_2\) | = | velocity of ball after impact, in m/s |
| \(T\) | = | torque at axis of rotation, in Nms |
| \(t\) | = | dwell time, or duration of impact, in seconds |
| \(v\) | = | linear velocity of the mass center, in m/s |
| \(v_1\) | = | linear velocity, just before impact, of racquet mass center, in meters/second |
| \(v_2\) | = | linear velocity, just after impact, of racquet mass center, in meters/second |
\(Mr^2 \div I\) is the Shock Factor, a dimensionless ratio that is a good indicator of general racquet quality. Note that another way of expressing this ratio is \(r \div q\). A low mass center radius (small \(r\)) is just as important as a high sweet spot (large \(q\)) for reducing Torque and Shock from impact. Therefore, a counterweight at the handle end (which gives small \(r\) and large \(q\)) should be effective, as the performance of the counterweighted Wilson Kannon proves.